Thomas Calculus || Exercise 8.1 || Question 01 to 05 || Basic Integration || Dadu Khan


Book.............👉👉👉....Thomas Calculus

Writer............👉👉👉....Thomas Finney

Edition..........👉👉👉....11th Edition

Chapter.........👉👉👉....No # 08

Name............👉......Technique of integration



(....Basic Integration Formulas....)


(.......Exercise 8.1.......)


Basic Substitutions........... 👇👇👇


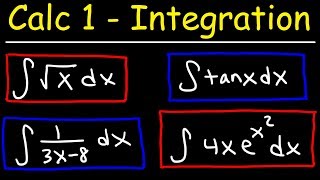
Questions.....No.....👉👉👉......(01 to 05)



#ThomasCalculus
#Chapter8
#DaduKhan
#DlCalculus
#Edition(11th)


Please Like, Share, Comments, Subscribe and press the bell icon on the YouTube app. Thank You Very Much.....😊🙂

Basic Integration 👇👇👇


In this method of integration by substitution, any given integral is transformed into a simple form of integral by substituting the independent variable by others. Take for example an equation having an independent variable in x, i.e. ∫sin (x3).


Let’s learn what is Integration before understanding the concept of Integration by Substitution. The integration of a function f(x) is given by F(x) and it is represented by:

∫f(x)dx = F(x) + C

Here R.H.S. of the equation means integral of f(x) with respect to x.

F(x) is called anti-derivative or primitive.
f(x) is called the integrand.
dx is called the integrating agent.
C is called constant of integration or arbitrary constant.
x is the variable of integration.
The anti-derivatives of basic functions are known to us. The integrals of these functions can be obtained readily. But this integration technique is limited to basic functions and in order to determine the integrals of various functions, different methods of integration are used. Among these methods of integration let us discuss integration by substitution.

Integration
Integration Rules
Integral Calculus
Integration by Parts
Integration by Substitution Method
In this method of integration by substitution, any given integral is transformed into a simple form of integral by substituting the independent variable by others.

Take for example an equation having an independent variable in x, i.e. ∫sin (x3).3x2.dx———————–(i),

In the equation given above the independent variable can be transformed into another variable say t.

Substituting x3 = t ———————-(ii)

Differentiation of above equation will give-

3x2.dx = dt ———————-(iii)

Substituting the value of (ii) and (iii) in (i), we have

∫sin (x3).3x2.dx = ∫sin t . dt

Thus the integration of the above equation will give

∫sin t . dt= -cos t + c

Again putting back the value of t from equation (ii), we get

∫sin (x3).3x2.dx = -cos x3 + c

The General Form of integration by substitution is:

∫ f(g(x)).g'(x).dx = f(t).dt, where t = g(x)

Usually the method of integration by substitution is extremely useful when we make a substitution for a function whose derivative is also present in the integrand. Doing so, the function simplifies and then the basic formulas of integration can be used to integrate the function.

When to Use Integration by Substitution Method?
In calculus, the integration by substitution method is also known as the “Reverse Chain Rule” or “U-Substitution Method”. We can use this method to find an integral value when it is set up in the special form. It means that the given integral is of the form:

∫ f(g(x)).g'(x).dx = f(u).du

Here, first, integrate the function with respect to the substituted value (f(u)), and finish the process by substituting the original function g(x).

Integration by Substitution Example
To understand this concept better, let us look into the examples